Day1: 1. Data Analysis
데이터 분석의 "모든 것"을 다루는 것이 우리 강연의 목표는 아닙니다. 데이터의 종류에 따라, 분야에 따라, 방법에 따라, 세상에는 너무나 많은 데이터 분석이 존재합니다. 다만 이 챕터에서 데이터 분석의 대강을 강연의 취지에 맞춰 나름대로 살펴보고 지나갑시다. 그리고 모두가 말하지만 그래서 그게 뭔지 알쏭달쏭한 "데이터 사이언스"에 대해서도요!
Descript and Infer the Structure
데이터 분석은 데이터의 "구조"를 분석하는 일입니다.
그리고 구조의 분석은 보통 "분포"의 구조를 분석하는 일입니다. 데이터 내의 값들이 어떻게 분포하는가? 평균은 어떻고 분산은 어떤가?
분포의 구조를 분석한다는 것은 달리 표현하면, 분포의 구조를 표현하는 여러 지표들을 측정하는 일이기도 합니다. 즉 분포의 평균(mean), 중앙값(median), 최빈값(mode), 그리고 분산(variance), 표준편차(standard deviation) 따위가 있습니다. 평균, 중앙값, 최빈값은 전체 값들을 대표할 수 있는 값이고, 분산과 표준편차는 값들이 (평균으로부터) 얼마나 떨어져 분포하는지 나타내는 값이죠.
이때 우리에게 주어진 데이터, 즉 표본(sample)의 구조를 표현하는 지표를 통계량(statistics)이라고 부릅니다. 표본평균, 표본표준편차 같은 것들이 해당되겠죠. 이처럼 표본의 통계량을 구하고 기술(Description)하는 일을 기술 분석이라고 부릅니다.
한편 어떤 표본은 그 표본이 수집되어 나온 모집단(population)을 대표하는(represent) 데이터이기도 합니다. 그리고 모집단의 분포의 구조를 표현하는 지표를 모수(parameter)라고 부릅니다. 모평균, 모표준편차 같은 것들이 되겠죠. 그런데 모집단 자체는 우리에게 알려져 있지 않기 때문에, 모집단의 모수는 기술할 수 없고 추론(inference)할 수 있을 뿐입니다. 이때 모집단의 모수를 추론하는 일을 추론 분석이라고 부릅니다.
기술과 추론: 사실 데이터 분석은 이게 다입니다! (아마도?)

A boring figure
표본이나 모집단, 그리고 각 통계량과 모수를 수학적 기호로 표현하는 방법이 단 하나로 정해져 있는 것은 아닙니다. 다만 대체로 표본과 모집단을 대비하여, 표본에는 알파벳 소문자, 모집단에는 알파벳 대문자를 많이 사용합니다. 위 그림에서는 표본의 집합을
y로, 모집단을Y로 표현했습니다.
Description
[110, 76, 131, 100, 102, ... 136, 75, 107, 130, 117]와 같은, 100개의 관측치(observation)를 가진 데이터가 주어져 있다고 합시다. 이를 어떤 서베이의 어떤 문항에 대한 응답값이라고 가정합시다. 예컨대 일정 기간 동안 뉴욕 지역 가구 100개의 에어컨 사용량이라고 합시다. 이 데이터는 에어컨을 가진 전체 뉴욕 지역 가구로부터 추출된 샘플(표본)입니다. 샘플의 크기(\(n\))는 100입니다.
히스토그램으로 표현한 이 샘플의 분포는 다음과 같습니다.
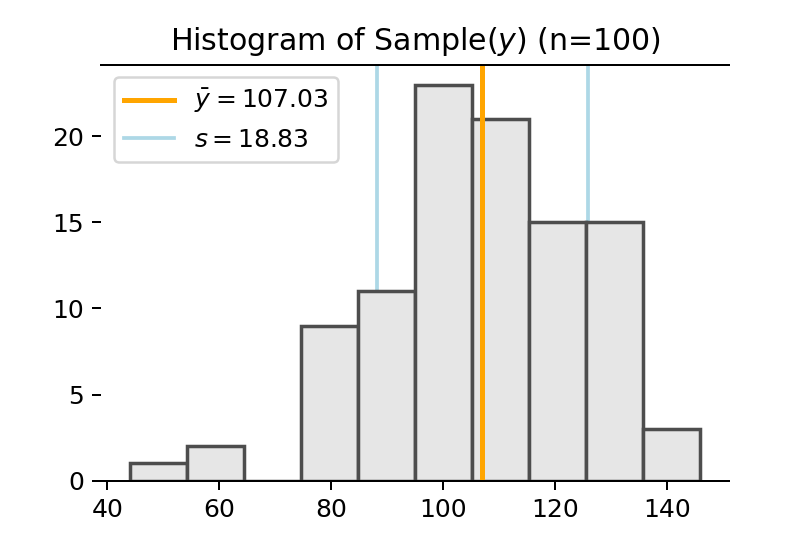
Distribution of Sample
이 샘플의 구조를 기술해 봅시다. 즉 분포의 구조를 나타내는 통계량들을 구해봅시다. 먼저 샘플의 평균, 즉 표본평균(\(\bar y\))은 107.17로 추정됩니다. 표본의 표준편차, 즉 표본표준편차(\(s\))는 18.84로 추정되네요. 분포의 모양새가 비대칭적이긴 하지만, 아무튼 전체적으로 관측치들이 107.17을 중심으로 평균적으로 18.84 정도 떨어져서 분포하고 있다고 표현할 수 있습니다.
사실 "표본표준편차"는 표본 내 관측치들 자체의 표준편차와는 값이 다릅니다. 표본표준편차를 구할 때는 각 관측치와 평균값 사이의 차를 샘플 수
n이 아닌n-1로 나눠주기 때문입니다. 여기에는 명확한 수학적 이유가 있지만, 넘어갑시다!
기본적인 기술분석은 이렇게 표본과 표준편차(또는 분산)를 보고하고, 샘플의 전체 수(여기서는 100)도 보고하고, 거기에 더해 필요하면 중앙값 같은 기타 통계량들을 함께 기술합니다. 또 하나! 전체 데이터의 분포를 나타내기 위해 히스토그램이나 KDE(kernel ensity estimation) 도표 같은 시각화 자료를 보고하기도 합니다. 이런 시각화 도표는 분석자 본인이 데이터의 분포를 확인하기 위해서도 유용하고, 다른 사람들에게 샘플의 구조를 직관적으로 전달하는 데에도 도움이 됩니다.
Inference
앞서 본 샘플은 각 응답자들이 추출되었던 더 큰 집단, 즉 모집단을 표현하는(represent)하는 집단입니다. 만일 랜덤하게 응답자들이 추출된 것이라면 (또한 샘플 크기가 충분히 크다면), 이 샘플은 모집단을 균일하게 대표한다고 가정해도 좋습니다.
우리의 예시에서 샘플의 모집단은 해당 기간 동안 에어컨을 보유하거나 사용했던 뉴욕 지역 가구 전체가 됩니다. (보다 엄밀히 말하면, 그 전체 가구들의 에어컨 사용량 값들의 집합입니다.)
사실 이 샘플은 예시를 위해 인위적으로 만든 모집단으로부터 랜덤하게 추출한 것입니다. 이 가상의 모집단의 분포를 히스토그램으로 나타내면 다음과 같습니다. 균형잡힌 대칭적인 모양새는 아니네요.
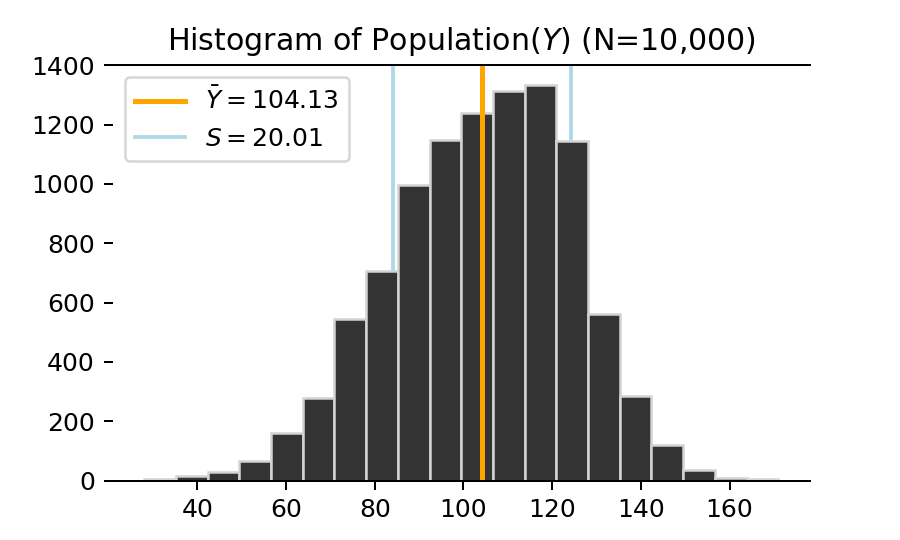
Distribution of Population
예시를 들기 위해 여기서는 인위적으로 모집단을 만들고 그로부터 샘플을 추출했지만, 실제 세계에서 우리는 어떤 샘플의 모집단에 대해 아무 것도 알지 못합니다. 모집단의 정확한 수조차 알기 어려운 경우가 많습니다. 다만 모집단으로부터 표집된 샘플을 알고 있을 뿐이죠.
따라서 우리는 모집단의 구조에 대해서는 직접적인 기술을 할 수 없고, 가정에 근거한 추론을 해야 합니다. 위 그림에는 모집단의 평균, 즉 모평균(\(\bar Y\))이 101.37이고 모표준편차(\(S\))는 20.88이라고 표시되어 있지만, 실제 세계에서 모집단을 모르는데 이런 모수들도 당연히 알 수 없습니다. 일정한 가정에 근거해 주어진 표본으로터 추론을 할 수 있을 뿐입니다.
가정에 근거한 추론을 하겠다는 것은 달리 표현해 각 모수들이 존재할 수 있는 분포를 추정하겠다는 것입니다. 예컨대 모집단의 평균, 즉 모평균(\(\bar Y\))을 추론하는 작업은 모평균이 존재할 수 있는 분포를 추정하는 작업이 됩니다.
그런데 통계학에서는 전통적으로 크게 두 가지의 서로 다른 추론법이 존재합니다. 하나는 빈도주의(frequentist) 접근법, 또 하나는 베이지안(bayesian) 접근법입니다. 혹자는 두 방법의 차이가 단지 기술적인 차이를 넘어 세계를 인식하는 철학적 차이를 나타낸다고 말하기도 합니다. 🤷
이 두 접근법의 차이를 잘 이해하고 다루는 것이 우리 강연의 목표는 절대 아닙니다. 하지만 가벼운 마음으로(!) 살짝 살펴보고 갑시다.
(1) Frequentist Approach
빈도주의 접근법에서는 모집단 자체의 분포는 크게 중요하지 않습니다. "중심극한정리(central limit theorem)"에 따라, 모집단의 분포가 어떤 모양새인가와는 상관없이, 모집단으로부터 추출된 "표본들의 평균"이 정규분포를 따른다고 알려져 있습니다. 즉 어떤 모집단으로부터 여러 번 표본을 추출하고, 각 표본의 평균들을 구해서 이 "표본평균의 분포"를 그려보면 그 분포가 정규분포를 따른다는 것입니다. 이때 표본평균의 평균 \(E(\bar y)\)은 이론상 모평균 \(\bar Y\)과 일치하게 됩니다.
한번 앞서 인위적으로 만든 모집단으로부터 여러번 표본을 추출해보고 표본평균의 분포를 살펴보겠습니다. 크기가 100인 샘플을 500회 뽑고, 각 회차마다의 표본평균을 모아서 히스토그램으로 분포를 나타내면 다음과 같습니다.

Distritbution of Sample Means
중심극한정리에 따라, 표본평균의 분포가 모평균을 평균으로 하는 정규분포에 매우 근사하고 있음을 알 수 있습니다.
그런데 사실 실제 세계에서 우리는 모집단에 대해서도 모르고, 당연히 표본평균의 분포, 즉 "여러 표본들의 평균의 분포"에 대해서도 알 수 없습니다. 실제 상황에서 우리가 알고 있는 것은 그저 단 하나의 표본뿐입니다. 결국 우리는 이 하나의 표본으로부터, "표본평균들의 (정규)분포"를 추정해야 합니다. 그리고 그 추정을 곧 모평균에 대한 추정으로 갈음해야 합니다.
결과적으로 - 이러저러한 공식과 가정에 따라 - 우리에게 주어진 어떤 표본이 크기가 \(n\)이고 표본평균은 \(\bar y\), 표본표준편차는 \(s\)일 때, 표본평균의 분포는 평균이 \(\bar y\), 표준편차가 (\(\frac{s}{\sqrt{n}}\))인 정규분포를 따른다고 추정할 수 있습니다. 표본평균에 대한 표현을 모평균에 대한 표현으로 갈음하면, 우리는 모평균의 추정치가 평균이 \(\bar y\), 표준편차가 (\(\frac{s}{\sqrt{n}}\))인 정규분포 상에 존재한다고 가정할 수 있습니다. 식으로 표현하면
\( \bar Y \sim N(\bar y, (\frac{s}{\sqrt{n}})^2) \\ \)
입니다. 단, 엄밀히 말하면 위 식은 모평균 자체가 아닌 모평균에 대한 추정치의 분포를 표현하고 있습니다. 이때 정규분포의 표준편차 \(\frac{s}{\sqrt{n}}\)는 모평균의 추정치에 대한 평균적인 오차의 크기를 나타내므로, 표준오차(Standard Error)라고 부르기도 합니다. (\(S.E = \frac{s}{\sqrt{n}}\))
어찌됐든 모평균의 추정치가 존재하는 정규분포를 구했기 때문에, 정규분포의 정의를 이용해 모평균의 추정치가 존재하는 일정한 구간을 "신뢰도"와 함께 표현할 수 있게 됩니다. 예컨대 모평균은 95%의 신뢰도로 \(\bar y - 1.96 S.E\) ~ \(\bar y + 1.96 S.E\) 구간 안에 존재한다고 가정할 수 있습니다. 앞서 본 예시 샘플의 경우, 모평균은 정규분포 \(N(107.17, 1.88^2)\)에서 추론되고, 95%의 신뢰도로 102.64~110.18 사이에 존재한다고 추정할 수 있습니다.
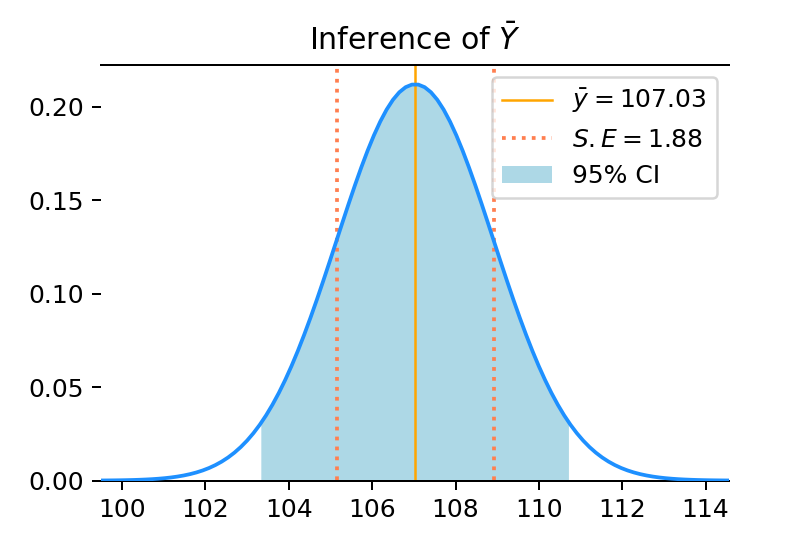
95% Confidence Interval
보통 통계적으로 모평균을 추론한다고 할 때 지금까지 살펴본 방법을 취하게 됩니다. 사실 대부분의 기본적인 통계추론 방법이 이와 같은 빈도주의 접근법에 기반하고 있기 때문에, 굳이 빈도주의라는 말조차 잘 사용하지 않습니다. 보통 베이지안과 비교할 때나 빈도주의라는 꼬리표롤 붙이게 됩니다. 빈도주의 접근법은 중심극한정리 등 그 수학적 근거가 잘 갖춰져 있고, 계산 과정이 비교적 간단하고 공식화되어 있다는 장점이 있습니다. 또 샘플 수가 충분히 크고 모집단으로부터 랜덤하게 추출된 경우, 모집단에 대한 충분히 효과적이고 편향되지 않은 추정치를 내놓을 수 있습니다.
그런데 이런 장점들의 한편으로 ... 어딘가 조금 tricky하게 느껴지지 않았나요? 사실 그렇습니다. 논리적으로 선후관계를 따져보면, 먼저 모집단이 존재하고, 그로부터 여러 개의 표본들이 존재할 수 있고, 그 가운데 하나의 표본이 있는 셈입니다. 그런데 실제로 벌어진 일은 하나의 표본으로부터 표본평균의 분포를 가정하고는, 그 표본평균의 분포가 곧 모평균의 분포라고 - 명시적으로 얘기하진 않지만 사실 그게 그거인 - 얘기를 하고 있습니다. 또한 빈도주의적 관점은 원칙적으로 모평균과 같은 모집단의 모수가 확률분포 상의 변수가 아닌 (알려져 있지 않지만) 고정된 상수라고 가정하며, 그렇기 때문에 "모평균의 분포"가 아닌 "모평균의 추정치의 분포"를 구하고 있다고 명목상 주장합니다. 하지만 사실상 확률변수로서의 모평균의 분포를 추정하고 있는 것과 다를 바가 일을 하고 있습니다. 논리적 모순이 완전히 해소되지 않았고, 보다 명확하게 해명해야 할 것 같은 전제와 연결고리들을 암묵적으로 넘겨버리는 찜찜함은 빈도주의적 접근법의 어쩔 수 없는 한계입니다.
(2) Bayesian Approach
베이지안 접근법은 베이즈 정리(Bayes' theorem)에 기초합니다.
어떤 사건 A와 B, 그리고 각 사건이 일어날 확률에 대해, 베이즈 정리는 다음과 같이 표현됩니다:
\[ Pr(A|B) = \frac{Pr(B|A) Pr(A)}{Pr(B)} \propto Pr(B|A) Pr(A) \]
사실 아주 간단한 정리입니다.
B가 주어졌을 때의 A의 "사후 확률"(\(Pr(A|B)\))은, A의 "사전 확률"(\(Pr(A)\))에, A가 주어졌을 때의 B의 "조건부 확률(likelihood)"(\(Pr(B|A)\))의 값의 곱에 비례한다는 것입니다. 여기서 B는 이미 알고 있는 관측된 대상이고, A는 사전에 가지고 있는 정보 및 B에 대한 정보를 가지고 알아내야 하는 대상입니다. 이때 B를 주어진 샘플, 그리고 A를 추정해야하는 모집단의 모수(parameter)라고 생각해 봅시다. 그렇다면 샘플이 주어졌을 때의 모수의 "사후 확률"을 구하는 것이 우리가 하고자 하는 추론 작업이 되고, 이는 모수에 대해 미리 가지고 있는 가정인 모수의 "사전 확률"과, 모수가 주어졌을 때의 관측된 샘플의 "조건부 확률"을 통해 구할 수 있다는 점을 짐작할 수 있습니다.
베이지안 모형을 이용해 모평균을 추정하기 위해서는 먼저 모집단의 분포를 어떤 확률분포로 가정해야 합니다. (빈도주의 접근법이 모집단의 분포에 대해서는 다소 무신경했던 것과 다릅니다.) 모집단의 특징에 맞게 확률분포를 가정하면 됩니다. 이 경우 정규분포를 가정해 봅시다.
\[ Y \sim N(\bar Y, S^2) \]
이 정규분포의 모수(parameter)는 \(\bar Y\)와 \(S\)입니다. 이때 이 모수들도 다시 자신의 사전분포를 가정할 수 있습니다. 그리고 사전분포의 모수를 실수로 지정해도 되지만, 다시 그 모수들이 자기 자신의 사전분포를 갖도록 설정할 수도 있습니다. 예컨대 \[ \bar Y \sim ~ N(\mu, \sigma^2) \\ S \sim N(10, 10^2) \] 같은 식입니다. 이 경우 \(\mu\)와 \(\sigma\)도 사전분포를 정의해야 겠네요.
베이지안 모형은 기본적으로 여러 번 반복 시행하면서 추정치를 업데이트하고 결과를 표집하는 모형입니다. 시행마다 추정해야 하는 모수들에 대한 값을 (이전 시행의 결과를 바탕으로) 랜덤하게 제시하면서, 그와 같은 모수가 주어졌을 때의 사전 확률 및 관측치(샘플)의 조건부 확률(우도)을 계산하고, 이를 바탕으로 사후 확률을 계산한 후, 이 사후 확률이 개선된 정도를 바탕으로 해당 값을 표집할지 안 할지, 즉 수용도를 결정합니다. 이런 과정을 반복하게 되면 주어진 조건, 즉 설정된 사전분포 및 관측치의 분포로부터 적합하게 설명될 수 있는 추정치들이 사후분포로 표집됩니다. 결과적으로 어떤 모수의 추정치가 표집된 사후분포를 가지고 해당 모수의 구조를 추론할 수 있게 됩니다. 예컨대 \(\bar Y\)의 사후분포의 평균을 \(\bar Y\)의 추정 평균값으로 사용할 수 있고, 또 사후분포의 평균(또는 중앙값)을 중심으로 95% 이내에 표집된 샘플들의 경계 구간이 곧 해당 모수의 95%의 확실성(certanty)를 갖는(=5%의 불확실성uncertanty)를 갖는 신용구간(credible interval)입니다. (빈도주의 접근과는 사용하는 용어가 살짝 다릅니다.)
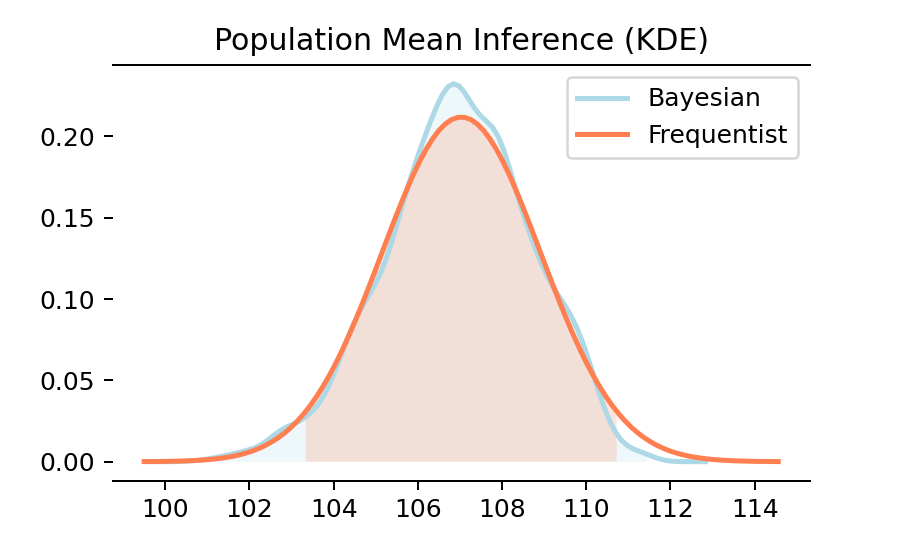
Frequentist VS Bayesian
빈도주의 접근과 베이지안 접근에 따른 모평균 추정치를 비교해 보면 결과가 거의 비슷합니다. 이처럼 간단한 추론 작업에서 빈도주의와 베이지안 모형의 차이는 거의 없습니다. 그렇기 때문에, 여러 번 반복 시행의 샘플링 과정을 거쳐야 하는 베이지안 보다는 비교적 간단한 공식으로 결과를 도출할 수 있는 빈도주의 모형이 즐겨 사용됩니다.
그럼에도 불구하고 베이지안 모형이 선호되는 경우는 언제일까요? 샘플 수가 비교적 적거나, 빈도주의 접근으로 정의하기에는 다소 복잡한 모형의 구조를 가정해야 하는 경우입니다.
예컨대 베이지안 모형은 여러 기관의 여론조사 결과를 수합해 일반화된 트렌트를 추출할 때 많이 사용됩니다. 이때 "실제 여론"이라는 모집단은, 각각의 여론조사라는 여러 개의 분할된 샘플을 통해 표현됩니다. 빈도주의 모형이라면 각각의 샘플들의 가중치 상수를 사전에 결정하고 모형에 통합해야 합니다. 반면 베이지안 모형에서는 각 샘플의 가중치 자체를 사전분포에 대한 가정으로 모형 내부에 통합할 수 있습니다. 이 경우 보다 합리적인 추론이 가능해집니다.
Tip. 눈치채셨을 지도 모르지만, "모평균"을 추론하는 일에 비해 "모표준편차"를 추론하는 일은 빈도주의 접근에서나 베이지안 접근에서나 사실 그렇게 큰 관심사가 아닙니다(...)
(3) Black Box
마지막으로 "Black Box" 모형을 살펴봅시다. 데이터 과학에서 어떤 "모형"은 인풋이 주어졌을 때 어떤 수식에 의해 인풋을 처리한 후 그에 따른 아웃풋을 반환하는 모형입니다. 즉
\( Output = Model(Input) \)
이라고 표현했을 때, \(Input\)을 \(Output\)으로 변환해주는 함수 \(Model\)이 어떤 모형이라고 할 수 있습니다. 만일 이 모형의 구조를 알고 있다면 이 모형은 블랙박스가 아닙니다. 앞서 본 빈도주의 접근이나 베이지안 접근에 따른 통계 모형들은 모형을 수식으로 설명할 수 있고, 모형이 작동하는 방식과 그 근거를 잘 설명할 수 있었습니다.
만일 어떤 모형이 인풋을 아웃풋으로 처리하긴 하지만, 모형 내부에서 데이터를 처리하는 방식을 일관되고 구체적인 방식으로 기술할 수 없다면 블랙박스 모형이라고 부를 수 있습니다.
모수(parameter)의 관점에서 생각해 봅시다. 빈도주의나 베이지안 모형은 각 모수에 특정한 이름을 붙일 수 있고 그 의미와 역할을 설명할 수 있었습니다. 하지만 블랙박스 모형에 들어있는 모수들은 보통은 (개별적인 이름 없이) 그냥 파라미터입니다.
모든 머신러닝 기법이 블랙박스 모형은 아니지만, 대체로 머신러닝 기법들은 블랙박스 모형에 가깝습니다. 많은 머신러닝 모형은 인풋을 아웃풋으로 변환하는 어떤 모형을 가정하고, 그 모형 내부의 파라미터를 반복적으로 업데이트하는 방식을 사용합니다. 초기값에 따른 아웃풋과 실제 아웃풋 사이의 차이를 최소화하는 방향으로 파라미터를 조정하는 것입니다.
그리고 이런 머신러닝 기법 중 가장 대표적인 사례가 바로 딥러닝입니다. 딥러닝은 인풋을 아웃풋으로 변환하기까지 여러 번의 행렬 연산을 거칩니다. 이때 각각의 행렬 속에 들어있는 요소들이 모형의 파라미터가 됩니다. (사실 딥러닝에서 파라미터를 업데이트하는 과정은 본질적으로 베이즈 정리에 기반합니다.)
예컨대 한국어 인풋 데이터와 영어 아웃풋 데이터가 주어졌을 때, 한국어 데이터는 딥러닝 모형 내 여러 층을 거치면서 영어 데이터로 변환되게 됩니다. 만일 모형이 잘 학습되었다면, 다른 한국어 데이터를 투입했을 때 그에 따른 좋은 영어 데이터가 결과로 출력될 것이라고 기대할 수 있습니다.
앞서 살펴봤던, 모집단의 모평균을 추론하는 것이 딥러닝을 사용할 만한 적절한 사례는 아닙니다. 사실 딥러닝과 같은 블랙박스 모형에서는 "샘플"과 "모집단"의 구분이 흐릿해집니다. 주어진 대규모의 인풋을 기대되는 아웃풋에 맞게 - 오차가 최소화되도록 - 잘 변환하는 것이 딥러닝 모형의 역할이지, 내부적으로 샘플과 모집단을 구별하고 모집단에 대한 가정을 세우고 하는 문제는 고려되지 않습니다.
다만 지금까지 살펴본 사례에 딥러닝 모형을 (어거지로) 적용해 봅시다. 모평균을 추정하기 위해서는 모집단을 추정해야 합니다. 그렇다면 주어진 샘플을 모집단으로 변환하는 모형, 즉 (\(Y = Model(y)\))과 같은 모형을 정의해야 합니다. 그런데 우리는 모집단은 모르기 때문에, 실제로는 (\(y = Model(y)\))과 같은 방식으로 모형을 학습해 보겠습니다. 합리적인 진술은 아니지만, 편의상 이 모형이 샘플을 모집단에 근사시키는 모형이라고 정의하겠습니다.
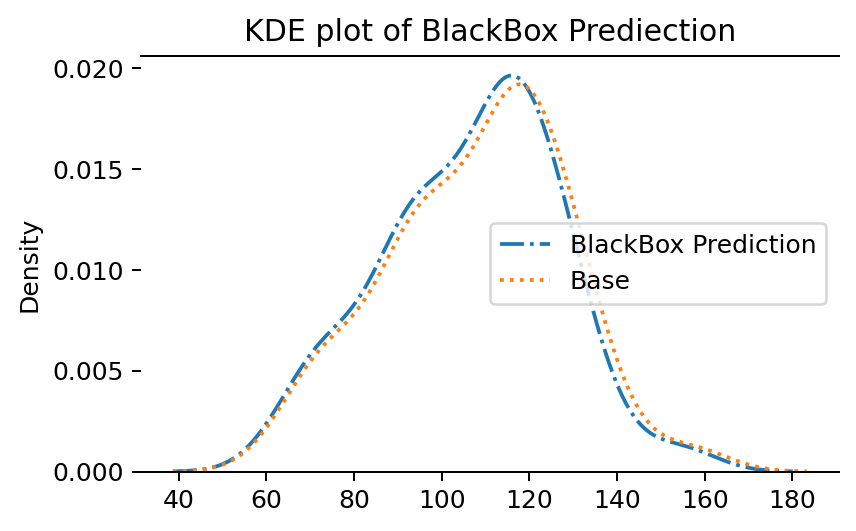
BlackBox Model
작은 딥러닝 모형을 학습시킨 후, 이 모형에 따른 샘플의 예측값(prediction)을 구해보고 실제 샘플의 분포와 비교해 보았습니다. 당연하게도(?) 예측값의 분포는 실제 샘플의 분포와 거의 일치합니다.
사실 이 딥러닝 모형이 실질적으로 수행하는 일은 거의 없습니다. 인풋을 거의 그대로 아웃풋으로 반환할 뿐입니다. 하지만 한국어 데이터 -> 영어 데이터와 같이 실질적인 변환을 수행해야 한다면, 그때에야 딥러닝 모형의 진가가 발휘될 것입니다.
에어컨 사용량과 같은 잘 정제된 샘플의 모평균을 구하는 목적으로 딥러닝 같은 블랙박스 모형을 사용하지는 않습니다. 블랙박스 모형은 주어진 데이터의 구조를 잘 알지 못하거나, 데이터의 구조가 복잡하고 비정형성이 커 명확한 모형으로 정의하기 어려운 경우에 주로 사용됩니다.
Wrap Up
지금까지 샘플로부터 모집단의 평균을 추론하는 비교적 간단한 사례를 살펴보았지만, 실제로는 보다 복잡한 추론 분석들이 가능할 것입니다. 예컨대 두 개의 변수 사이의 관계를 추론하고자 할 때, 두 변수 사이의 관계를 표현하는 수식을 가정하고 그 수식을 표현하는 모수를 추론하는 과정을 거치게 됩니다. 물론 딥러닝 같은 블랙박스 모형이라면 수식을 가정하지 않은 채 바로 모형을 학습할 것입니다.
각 접근법들은 언제나 서로 무 자르듯 구별되지 않으며, 각 접근법 내에서도 더욱 다양한 기법과 관점이 존재할 수 있습니다. 다만 "데이터의 구조를 분석"하는 것이 데이터 분석이라는 점을 상기했을 때, 각 접근법의 차이는 다루는 데이터의 구조의 차이를 반영하는 것이라고 생각할 수 있습니다.

What to do?
잘 정제된 데이터만 분석할 수 있던 시절에는 빈도주의 접근에 기반한 통계학 기법들을 잘 사용하는 것으로 충분했습니다. 어떤 이유로 보완이 필요하다면 베이지안 기법을 함께 사용할 수 있었습니다. 하지만 텍스트 데이터와 같이 비정형적이고 그 구조를 가정하기 어려운 데이터들이 빅데이터의 형태로 공급되고, 그러한 빅데이터를 처리하고 분석해야할 필요성이 높아지면서 우리는 머신러닝/딥러닝의 세계로 나아가야 했습니다.
흔히 통계학이라고 부르던 전통적인 맥락의 데이터 분석이 (주로) 빈도주의 접근법 그리고 베이지안 접근법을 취해왔다면, 오늘날 "데이터 사이언스"라고 불리는 영역은 그러한 전통적 통계학 기법은 물론이고(!) 빅데이터를 다루는 방법 그리고 머신러닝/딥러닝을 이용해 빅데이터를 처리하는 방법들까지 망라하게 된 것입니다.
"Data Science"
그래서 "데이터 사이언스"는 대체 무슨 뜻일까요? 아마 모두가 만족할 만한 하나의 정의를 내리기는 어려울 것 같습니다. 차라리 데이터 사이언스는 "그 모든 것"입니다. 데이터 분석을 하기 위해 필요한 모든 것들. 전통적인 통계학 지식은 물론이고, 빅데이터가 등장함으로서 필요하게 된 (데이터를 관리하고 처리하기 위한 각종 하드웨어/소프트웨어) 컴퓨팅 능력과 (빅데이터 같은 비정형 데이터를 잘 다루기 위한) 미신러닝/딥러닝, 그리고 이 모든 것들을 의미있게 사용하기 위한 필드 전문성까지.
데이터 사이언스에는 이 모든 것이 들어있고, 모든 것을 잘 할 수 있다면 좋겠지만 현실적으로 그렇기는 어렵기 때문에, 사람마다 저마다의 데이터 사이언스를 하는 셈입니다.
그런데 과거에도 "데이터 마이닝" 같은 말이 유행한 적이 있었습니다. 데이터 마이닝도 데이터 사이언스처럼 뭐라고 시원하게 정의하기는 어렵고, 굳이 이 둘을 비교하는 것이 억지스러울 수는 있습니다. 그럼에도 불구하고 과거의 데이터 마이닝과 근래의 데이터 사이언스를 구별짓는 가장 큰 차이는 역시 "분야(field) 전문성"이라고 생각됩니다. "데이터 사이언스 분야에서의 전문성"을 뜻하는 게 아닙니다. "자기 분야에서의 전문성"을 뜻하는 것입니다. 결국 데이터 분석은 도구적 작업입니다. 그 자체가 고유한 필드 이론을 가진 하나의 분야는 될 수 없습니다. 자기 분야에서의 전문성과 이론적 토대를 가지고, 어떤 질문에 답하기 위해 어떤 데이터를 어떻게 활용하고 어떻게 분석할지 스스로 결정하고 수행할 수 있는 능력이 중요합니다.
그래서 데이터 마이니스트는 없지만 데이터 사이언티스트는 있을 수 있습니다. 이때 좋은 데이터 사이언티스트는 단지 각종 분석 도구를 섭렵하고 각종 분석 방법을 사용할 수 있는 사람이 아니라, 자기 분야의 이론적 자원을 가지고 자신이 필요한 문제에 맞는 분석 도구와 방법을 찾아서 사용할 수 있는 사람일 것입니다.
인문/사회과학 연구자들 중 빅데이터나 데이터 사이언스를 연구에 접목하는 이들 가운데는, 흔한 오해와 달리 양적 분석에만 집중하는 것이 아니라 질적 분석과 이론적 탐구에도 함께 집중하는 경우를 많이 볼 수 있습니다. 빅데이터와 같은 구조화되지 않은 비정형 데이터를 잘 다루고 분석하기 위해서는 결국 근거가 될만한 이론이 필요하기 때문입니다. 또 어떤 빅데이터들 - 예컨대 수백년 동안의 문헌 데이터 - 들은 그 자체로 실증적으로 검증하기 어려웠던 이론을 검증해 볼 수 있는 기회를 제공하기도 합니다.
빅데이터, 머신러닝, 데이터 사이언스 ... 결국 중요한 것은 기법 그 자체가 아니라 스스로 질문을 정의할 수 있고 답을 찾아갈 수 있는 능력입니다.🔍